Fungsi dan Pemetaan
 Relasi dan Fungsi
Relasi dan Fungsi
• Relasi antara himpunan A dan B Pemasanagan anggota himpunan A dengan anggota himpunan B berdasarkan aturan tertentu. • Penyajian Relasi himpunan A dan B Relasi dapat disajikan dengan : (1) diagram panah, (2) diagram kartesius, (3) himpunan pasangan berurutan. • Pemetaan atau fungsi Pemetaan atau fungsi adalah relasi dari himpunan A ke B yang memasangkan setiap anggota A dengan tepat satu anggota B. • Syarat-syarat pemetaan dan Fungsi
Pada diagram panah
- Semua anggota A mempunyai pasangan di B - Tidak ada satupun anggota A yang berpasangan dengan lebih dari satu anggota B
Pada diagram kartesius
- Semua anggota A mempunyai pasangan di B (ditandai dg titik koordinat) - Tidak ada dua atau lebih titik koordinat yang yang segaris vertikal (keatas)
Pada himpunan pasangan berurutan
- Semua anggota A ditulis sekali pada setiap pasangan
Contoh Pemetaan:
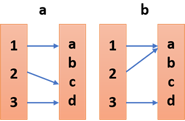
Pada contoh (a) berlaku :
- {1,2,3} disebut domain (daerah asal)
- {a,b,c,d} disebut kodomain (daerah kawan}
- (a,c,d} disebut range (daerah hasil)
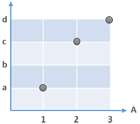 {(1,a) , (2,c) , (3,c)}
{(1,a) , (2,c) , (3,c)}
Contoh Bukan pemetaan:
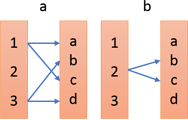
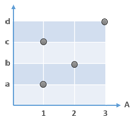 {(1,a) , (1,c) , (2,b) , (3,d)}
{(1,a) , (1,c) , (2,b) , (3,d)}
 Notasi pemetaan/fungsi
Notasi pemetaan/fungsi
Sebuah fungsi f memasangkan setiap x anggota A dengan y anggota B dituliskan notasinya adalah f : x -> y dibaca "fungsi f memetakan x ke y". y disebut bayangan atau peta dari x oleh fungsi f atau dapat ditulis dalam bentuk rumus f(x) = y. • Jika banyaknya anggota A adalah n(A) dan banyaknya anggota B adalah n(B) maka banyaknya pemetaan yang mungkin dibuat dari A ke B adalah = n(B)n(A) dan banyaknya pemetaan yang mungkin dibuat dari B ke A adalah = n(A)n(B) • Korespondensi satu-satu antara himpunan A dan B adalah jika setiap anggota A mempunyai pasangan hanya satu anggota B dan setiap anggota B hanya berpasangan dengan satu anggota A. • Jika n(A) = n(B) = k maka banyaknya korespondensi satu-satu yang mungkin dibuat dari A ke B adalah = 1 x 2 x 3 x 4 x ... x k
