Peluang

Rumus Peluang dalam Matematika

Definisi:
Peluang adalah sebuah cara yang dilakukan untuk mengetahui kemungkinan terjadinya sebuah peristiwa.

Istilah istilah yang sering digunakan:

• Ruang Sampel
Merupakan himpunan dari semua hasil percobaan yang mungkin terjadi.
• Titik Sampel
Merupakan anggota yang ada di dalam ruang sampel
• Kejadian
Merupakan himpunan bagian dari ruang sampel.

Rumus Peluang Matematika

Frekuensi merupakan perbandingan antara banyaknya percobaan yang dilakukan dengan banyaknya kejadian yang diamati.

Rumus Frekuensi:

Frekuensi Relatif = Banyaknya kejadian : Banyaknya Percobaan.
Apabila setiap titik sampel dari anggota ruang sampel S mempunyai peluang yang sama, maka peluang kejadian K yang jumlah anggotanya dinyatakan dalam n(K) dapat diketahui dengan cara:
P(K) = nK / nS dengan K ⊂ C

Peluang munculnya kejadian dapat diperkirakan melalui notasi di bawah ini:
0 ≤ P(K) ≤ 1
• Apabila nilai P(K) = 0 maka kejadian K tersebut sangat mustahil untuk terjadi
• Apabila nilai P(K) = 1 maka kejadian K tersebut pasti akan terjadi

Contoh Soal

Pada proses pelemparan sebuah dadu, tentukanlah peluang munculnya mata dadu yang berangka ganjil
Jawab:
Ruang sampel S = {1,2,3,4,5,6}
n(S) = 6
Mata dadu ganjil = {1,3,5}
n(S) = 3
maka P(K) = 3/6 = 1/2

Kejadian Majemuk

Kejadian majemuk adalah dua atau lebih kejadian yang dioperasikan sehingga terbentuklah sebuah kejadian yang baru
Suatu kejadian K dan kejadian komplemen berupa K' memenuhi persamaan:
P(K) + P(K') = 1 atau P(K') = 1 - P(K)

Contoh Soal

Seperangkat kartu bridge, diambillah satu buah kartu secara acak. tentukan peluang terambilnya kartu yang bukan As.

Jawab:
Jumlah kartu bridge = n(S) = 52
Jumlah kartu As = n(K) = 4
P(K) = 4/52 = 1/13

peluang yang terambil bukan kartu As = P(K') = 1-P(K) = 1 - 1/13 = 12/13

Penjumlahan Peluang

Kejadian Saling Lepas

Dua buah kejadian A dan B dikatakan saling lepas apabila tak ada satupun elemen pada kejadian A yang sama dengan elemen yang ada pada kejadian B. Untuk dua buah kejadian yang saling lepas, maka peluang salah satu A atau B mungkin terjadi, rumusnya adalah:
P(A ∪ B) = P(A) + P(B)

Contoh Soal

Dua buah dadu masing-masing berwarna merah dan hitam dilempar secara bersamaan sebanyak satu kali, tentukanlah peluang munculnya mata dadu yang berjumlah 3 atau 10.
Jawab:
Hasil pelemparan dadu tersebut sbb:

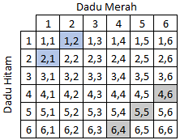Kejadian mata dadu berjumlah 3 ditandai dengan warna biru. A = {(1,2), (2,1)}
n(A) = 2
Kejadian mata dadu berjumlah 10 ditandai dengan warna biru
B = {(4,6), (5,5), (6,4)}
Karena tidak ada elemen yang sama pada A dan B digunakan rumus:
P(A u B) = P(A) + P(B)
P(A u B) = 2/36 + 3/36
P(A u B) = 5/36

Kejadian Tidak Saling Lepas

Artinya ada elemen A yang sama dengan elemen B, rumusnya dapat dituliskan:
P(A u B) = P(A) + P(B) - P(A n B)

Contoh Soal

Sebuah kartu diambil dari tumpukkan kartu bridge, tentukan peluang dari kartu yang terambil adalah kartu hati dan kartu bergambar (K,Q,J)
Jawab:
Jumlah kartu bridge = n(S) = 52
jumlah kartu hati = n(A) = 13
jumlah kartu bergambar = n(B) = 12

karena ada kartu bergambar yang merupakan kelompok kartu hati (J hati, Q hati, dan K hati) maka A dan B tidak saling lepas sehingga digunakanlah rumus:
P(A u B) = P(A) + P(B) - P(A n B)
= 13/52 + 12/52 - 3/52
= 22/52 = 11/26

Kejadian Saling Bebas

Dua buah kejadian dapat disebut saling bebas bila munculnya kejadian A tidak berpengaruh pada munculnya kejadian B sehingga peluang kejadian A dan B terjadi bersamaan dapat dituliskan menjadi:
P(A n B) = P(A) x P(B)

Contoh Soal

Pada percobaan pelemparan dua buah dadu, tentukan peluang munculnya angka genap pada dadu pertama dan angka ganjil prima pada dadu kedua.
Jawab:
Misalkan A = kejadian munculnya mata dadu genap pada dadu pertama = {2,4,6} maka P(A) = 3/6
Misalkan B = kejadian munculnya mata dadu ganjil prima pada dadu kedua = {3,5} maka P(B) = 2/6
karena kejadian A tidak berpengaruh pada kejadian B maka digunakan rumus:
P(A n B) = P(A) x P(B)
P(A n B) = 3/6 x 2/6 = 1/6

Kejadian Bersyarat

Kejadian bersyarat terjaid apabila kejadian A mempengaruhi munculnya kejadian B atau sebaliknya. maka dapat dituliskan seperti ini:
P(A n B) = P(A) x P(B/A)
atau
P(A n B) = P(B) x P(A/B)

Contoh Soal

Ada sebuah kotak yang berisi 5 bola merah dan 4 bola hijau. bila diambil dua buah bola satu persatu tanpa adanya pengembalian, tentukanlah peluang bola yang terambil adalah bola merah pada pengambilan pertama dan bola hijau pada pengambilan kedua.

Jawab:
Pada pengambilan pertama tersedia 5 bola merah dari 9 bola yang ada.
Maka P(M) = 5/9
Pada pengambilan kedua ada 4 bola hijau dari 8 bola yang tersisa (dengan syarat bola merah telah terambil).
Maka P(H/M) = 4/8
Karena kejadiannya saling berpengaruh, digunakanlah rumus:
P(M n H) = P(M) x P(H/M)
P(M n H) = 5/9 x 4/8 = 5/18