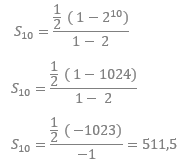Dereet

Dasar Barisan dan Deret Aritmetika

Diberikan sebuah barisan aritmetika sebagai berikut:
- 4, -1, 2, 5, 8, .....
Tentukan:
a) suku pertama
b) beda
c) jenis barisan
d) rumus umum suku ke-n kemudian cocokkan rumus dengan suku ketiga
e) suku kesembilan
f) jumlah 12 suku pertama

Pembahasan:

a) Suku pertama
a = -4

b) Beda
b = U2 - U1
b = -1 -(-4)
b = 3

c) Jenis barisan
Barisan aritmetika naik

d) Rumus umum suku ke-n
U_n = a + (n-1) b
U_n = -4 + (n-1) 3
U_n = -4 + 3n - 3
U_n = 3n - 7

e) Suku ketiga adalah 2, ceck
U_n = 3n - 7
U₃ = 3(3) - 7
U_n = 9 - 7 = 2
Cocok.

e) Suku kesembilan
U_n = 3n - 7
U₉ = 3(9) - 7
U_n = 27 - 7 = 20

f) Jumlah 12 suku pertama

- Jika diketahui suku pertama (a) dan suku terakhir yang hendak dihitung gunakan
Sn = n/2 (a + Un)

- Jika diketahui suku pertama dan beda tanpa harus mencari suku terakhir yang hendak dihitung gunakan
Sn = n/2 [2a + (n-1)b]

Dengan rumus yang kedua dimana:
a = -4
b = 3
n = 12
Sn = n/2 [2a + (n-1)b]
S₁₂ = 12/2 [2(-4) + (12-1)3]
S₁₂ = 6 [-8 + 33]
S₁₂ = 6 (25) = 150

Barisan dan Deret Geometri / Deret Ukur

Diberikan sebuah deret geometri sebagai berikut:
¹/₂, 1, 2, 4, 8, 16,...

Tentukan:
a) suku pertama deret di atas
b) rasio
c) Rumus suku ke-n, kemudian cocokkan dengan menggunakan suku ketiga
d) jumlah 10 suku pertama dari deret di atas

Pembahasan:

a) suku pertama
Suku pertama adalah a = ¹/₂
b) rasio
Mencari rasio pada deret geometri dengan membagi suatu suku ke-n dengan suku sebelumnya. Misalkan diambil suku keempat (4), maka dibagi dengan suku ketiga (2)
r = 4 / 2 = 2

c) Rumus suku ke-n setelah itu cocokkan dengan menggunakan suku ketiga
Rumus umum dari deret geometri adalah
Un = ar^n-1
Dengan data yang sudah diperoleh di atas maka
Un = ¹/₂ (2)^n-1
Cocokkan dengan n = 3
U₃ = ¹/₂ (2)^3-1
U₃ = ¹/₂ (2)²
U₃ = ¹/₂ (4) = 2

d) jumlah 10 suku pertama dari deret di atas Rumus Umum mencari jumlah hingga n suku

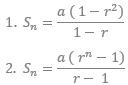Rumus yang pertama digunakan jika rasio lebih dari 1, rumus kedua jika rasio kurang dari satu.
Dengan rumus yang pertama:
n = 10
a = ¹/₂
r = 2