Sudut dan Garis
 Menghitung besar sudut pada bidang datar
Menghitung besar sudut pada bidang datar
Persegi Panjang & Persegi
• Jumlah besar keempat sudutnya = 360o • Dua sudut yang berhadapan sama besar = 90o
Segitiga
• Jumlah ketiga sudutnya = 180o
Jajaran Genjang
• Jumlah besar keempat sudutnya = 360o • Dua pasang sudut yang berhadapan sama besar • Dua pasang sisi yang berdekatan jumlahnya = 180o
Trapesium
• Jumlah besar keempat sudutnya = 360o • ∠ ADC+ ∠ DAB = 180o dan ∠ ABC + ∠BCD = 180o
Belah Ketupat
• Jumlah besar keempat sudutnya = 360o • Dua pasang sudut yang berhadapan sama besar
Layang-layang
• Jumlah besar keempat sudutnya = 360o • Sepasang sudutnya sama besar ? ∠DAB = ∠DCB
 Besar sudut pada garis yang berpotongan
Besar sudut pada garis yang berpotongan
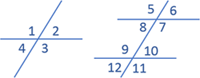
• Bertolak belakang : ∠ 1 = ∠ 3 ∠ 2 = ∠ 4 • Berpelurus : ∠ 1 + ∠ 2 = 180o ∠ 2 + ∠ 3 = 180o ∠ 3 + ∠ 4 = 180o ∠ 4 + ∠ 1 = 180o • Sehadap : ∠ 5 = ∠ 9 ∠ 6 = ∠ 10 ∠ 8 = ∠ 12 ∠ 7 = ∠ 11 • Dalam sepihak : ∠ 7 + ∠ 10 = 180o ∠ 8 + ∠ 9 = 180o • Luar sepihak : ∠6 + ∠ 11 = 180o ∠ 5 + ∠ 12 = 180o • Dalam berseberangan : ∠ 7 = ∠ 9 ∠ 8 = ∠ 10 • Luar berseberangan : ∠ 6 = ∠12 ∠5 = ∠11
 Sudut pusat, sudut keliling lingkaran
Sudut pusat, sudut keliling lingkaran
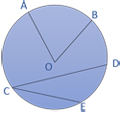
• Sudut pusat: Pada sebuah lingkaran adalah sudut yang terbentuk dari dua buah jari-jari lingkaran dengan titik sudutnya adalah titik pusat lingkaran. • Sudut keliling Adalah sudut pada lingkaran yang terbentuk dari dua buah tali busur yang berpotongan tepat pada keliling lingkaran. • Sudut AOB (∠AOB) adalah sudut pusat dengan titik sudut O (O juga sebagai titik pusat lingkaran) • Sudut DCE (∠ DCE) adalah sudut keliling dengan titik sudut C yang berada pada keliling lingkaran
Hubungan antara sudut pusat dan sudut keliling
Besarnya sudut pusat sama dengan dua kali besarnya sudut keliling yang menghadapi busur yang sama atau Besarnya sudut keliling sama dengan setengah kali besar sudut pusat yang menghadapi busur yang sama.
Perhatikan gambar dibawah ini:
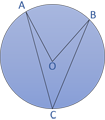 • ∠ AOB -> sudut pusat menghadapi busur AB
• ∠ ACB -> sudut keliling menghadapi busur AB, karena kedua sudut menghadapi busur yang sama yaitu busur AB maka berlaku :
∠ ??? = 2 x ∠ ACB atau
∠ ACB = 1/2 x ∠ AOB
• ∠ AOB -> sudut pusat menghadapi busur AB
• ∠ ACB -> sudut keliling menghadapi busur AB, karena kedua sudut menghadapi busur yang sama yaitu busur AB maka berlaku :
∠ ??? = 2 x ∠ ACB atau
∠ ACB = 1/2 x ∠ AOB
Sifat sudut keliling
- Sebuah sudut keliling yang menghadapi diameter lingkaran merupakan sudut siku-siku (90o) - Dua sudut keliling yang menghadapi busur yang sama adalah sama besar.
Segiempat talibusur
Adalah segiempat yang terbentuk dari empat buah tali busur yang berpotongan pada keliling lingkaran.
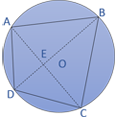
Sifat sifat Segiempat talibusur
- Jumlah besar dua sudut yang berhadapan pada segiempat talibusur sama dengan 180o ∠ABC + ∠ ADC = 180o ∠ DAB + ∠ BCD = 180o - Hasil kali diagonal-diagonalnya sama dengan jumlah perkalian sisi-sisi yang berhadapan (sifat Ptolomeus) AC x BD = (AB x CD) + (AD x BC) - Hasil kali bagian-bagian diagonalnya sama AE x EC = DE x EB
Sudut antara dua tali Busur
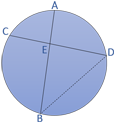
• Sudut Dalam Adalah sudut yang terbentuk karena dua tali busur berpotongan di dalam daerah lingkaran. Besarnya sudut dalam sama dengan jumlah dua sudut keliling yang menghadapi busur yang terletak diantara kaki-kaki sudutnya. - Talibusur AB berpotongan dengan talibusur CD di titik E yang terletak di dalam daerah lingkaran, maka sudut CEB dan sudut AED disebut sudut dalam. Karena kedua sudut saling bertolak belakang maka besar kedua sudut sama. ∠ CEB : sudut dalam menghadapi busur CB ∠ AED : sudut dalam menghadapi busur AD ∠ CDB : sudut keliling menghadapi busur CB ∠ ABD : sudut keliling menghadapi busur AD, maka berlaku : ∠ CEB = ∠ AED = ∠ CDB + ∠ ABD.
• Sudut Luar
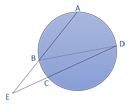 Adalah sudut yang terbentuk karena dua tali busur berpotongan di luar daerah lingkaran. Besarnya sudut luar sama dengan selisih dua sudut keliling yang menghadapi busur yang terletak diantara kaki-kaki sudutnya.
Talibusur AB berpotongan dengan talibusur CD di titik E yang terletak di luar daerah lingkaran, maka sudut AED dan sudut BEC disebut sudut luar. Karena kedua sudut berimpit maka besar kedua sudut sama.
∠ BEC : sudut luar menghadapi busur BC
∠ AED : sudut luar menghadapi busur AD
∠ CDB : sudut keliling menghadapi busur BC
∠ ABD : sudut keliling menghadapi busur AD, maka berlaku :
∠ BEC = ∠ AED = ∠ ABD - ∠ BDC
Adalah sudut yang terbentuk karena dua tali busur berpotongan di luar daerah lingkaran. Besarnya sudut luar sama dengan selisih dua sudut keliling yang menghadapi busur yang terletak diantara kaki-kaki sudutnya.
Talibusur AB berpotongan dengan talibusur CD di titik E yang terletak di luar daerah lingkaran, maka sudut AED dan sudut BEC disebut sudut luar. Karena kedua sudut berimpit maka besar kedua sudut sama.
∠ BEC : sudut luar menghadapi busur BC
∠ AED : sudut luar menghadapi busur AD
∠ CDB : sudut keliling menghadapi busur BC
∠ ABD : sudut keliling menghadapi busur AD, maka berlaku :
∠ BEC = ∠ AED = ∠ ABD - ∠ BDC
